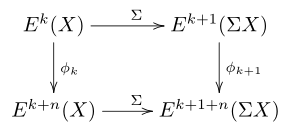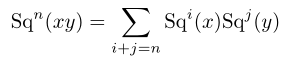Let’s begin by talking about cohomology operations.
Cohomology Operations
I will state a few definitions and results now, and explain their significance in a bit.
Definition: Let
and
be cohomology theories. A cohomology operation of “type
and degree
” is a natural transformation
. A stable cohomology operation of degree
is a collection of homomorphisms
of type
and degree
such that the following diagram commutes.
Because of Brown representability for ordinary cohomology and the Yoneda lemma, we observe that cohomology operations are in bijection with elements of
. (To expand on this: if
, then natural transformations
are in bijection with elements of
. To see this, consider
. Let the corresponding element of
be
. Given an element
of
, we define
via
.)
Theorem: Let
. There are stable cohomology operations
such that:
and
if
.
- The Cartan formula holds:
These are called the Steenrod operations.
The Adem relations hold as can be checked by the reader:
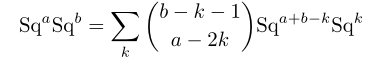
if . Let
be a sequence of positive integers. Define
. Inspired by the Adem relations, say that
is admissible if
for all
. In particular, this means that no Adem relations can be applied.
Theorem: The algebra of stable cohomology operations in
-cohomology is the quotient of the free associative
-algebra
by imposing the Adem relations. Equivalently, it is the
-algebra generated by
for admissible
. This is called the Steenrod algebra, and is denoted
.
Say that is indecomposable if it cannot be expressed as
for
having degree lower than that of
. What are the indecomposable elements of the mod
Steenrod algebra?
Example: Suppose . Then
is indecomposable. Let’s write
. The Cartan formulas tell us that
is a homomorphism of graded rings. In particular,
. We know that
where
. We compute that
, because all the higher terms vanish. This is
, by the characterization of Steenrod squares. In particular,
. Because
is a power of
, this is
. What this means is that
if
, and
. Consequently,
can’t be written as a composition of lower degree terms, and thus
is indecomposable.
It turns out:
Proposition: The
are the only indecomposables in
.
Proof. Consider for
, so that, in particular,
. We want to write
as the sum of lower degree terms. This follows from the Adem relations, because:
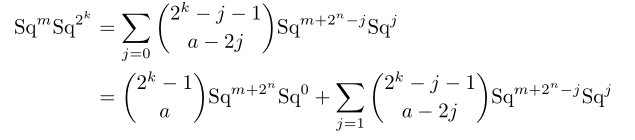
Now, , so:
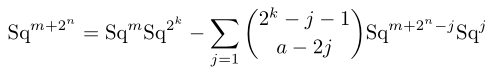
And hence is decomposable. QED.
This means that generates
as an algebra. I now want to give an application of Steenrod squares to a classical question in algebraic topology.
Vector fields on spheres
Recall the following classical result.
Proposition: Any vector field on
for odd
vanishes at some point. Moreover, there is a nowhere vanishing vector field on
for any even
.
Proof. Consider a point and a tangent vector
. The unit circle in the plane spanned by
and
is defined by
where
. As
goes from
to
, we get a homotopy between the antipodal map and the identity map. Looking at the degree tells us that
, i.e.,
is even and
is an odd-dimensional sphere.
Now suppose is even, so that
is odd-dimensional. Consider
, and write
. We need to construct a vector
such that
. An obvious choice is just
because then
. This is clearly continuous, and gives the desired vector field. QED.
A question that is now natural to ask, and has motivated a lot of algebraic topology, is the following.
Question: How many linearly indepedent vector fields exist on
? Namely, what is the maximum number of vector fields
on
such that
are all linearly independent for every
?
By Gram-Schmidt orthonormalization, the vectors can be replaced by
that span the same subspace of
. Gram-Schmidt orthonormalization is continuous, and thus we get vector fields
on
.
Consider the Stiefel manifold of orthonormal
-frames (ordered collection of
orthonormal vectors) in
. This can be topologized as a subspace of
. This is equivalently the space of
-matrices with orthonormal columns. For example,
. There is a map
given by projection onto the first factor.
Suppose there are linearly independent vector fields on
. There is a map
sending
, that is clearly a section of
. If one has a map
that is a section of
, then there are vector fields
defined via
. We want to therefore find some
such that for every
, there is no continuous map
that is a section of
.
Let’s look at a special case of this problem.
Definition: A manifold
is parallelizable if its tangent bundle is the trivial bundle.
In other words, if ,
is parallelizable if there are vector fields
such that
form a basis for the tangent space
at every point
of
.
Recall that acts on
by rotations. Suppose
is parallelizable. Then there is a section
of
. We can now consider the composition
, denoted
.
Let denote the standard basis vector
. Then
because
acts on
by sending it to
where
and the
are obtained from
as above. Also, by definition,
under
. Since
is parallelizable, we can consider
vector (linearly indepedent) fields
defined by
. We can assume that
are the other standard basis vectors
by changing signs if necessary, and “straightening” things out near
. Thus
is a multiplication on
with
as the identity. This is a H-space structure on
.
Lemma:
is a division algebra if and only if
is a H-space.
Proof. Define a multiplication via
. QED.
Studying H-spaces through the Hopf invariant
Construction: Suppose
, so that
. Its cofiber is the pushout
. Suppose that
. Then it is easy to see that
. Suppose
generates
and
generates
. Then
, so
for some integer
. This is called the Hopf invariant of
.
Example: Suppose is odd. Because of graded commutativity, it follows that
, so that
.
Proposition [Prop 4B.1 in Hatcher]: The Hopf invariant gives a homomorphism
.
It’s rather easy to see that the Hopf invariant of is
, and that the Hopf invariant of
is
. More interesting is the statement that we can find a map
whose Hopf invariant is
for even
. Consider
where
is a chosen basepoint. This has one cell in dimensions
. Thus it’s of the form
for some
, and Proposition 3.22 of Hatcher shows that
.
Suppose is a H-space structure on
. We will define a map
as follows. We know that
, which is
. On the first factor, define
, and on the second factor, define
.
Lemma: The Hopf invariant of
constructed above is
.
Proof. Claim 2.6 in http://math.uchicago.edu/~may/REU2015/REUPapers/Kirsche.pdf. QED.
Now we can prove the following important result.
Theorem: If
has Hopf invariant
, then
is a power of
.
Proof. Recall that . But
. If
was decomposable, then
, so
. Thus by our characterization of indecomposables in
, we know that
for some
. QED.
This means that if , then
isn’t parallelizable.
Theorem (Adams): If
has an element of Hopf invariant
, then
, or
.
Proof. K-theory, which we will proceed to study.